今日、生徒さんが、二桁の数を9で割ると、十の位と、一の位を入れ替えても、必ず、あまりが同じ数になると発見したので、そのことを考えてみた。
その子は八歳だから、そういうことを思いつくだけで、素晴らしい。
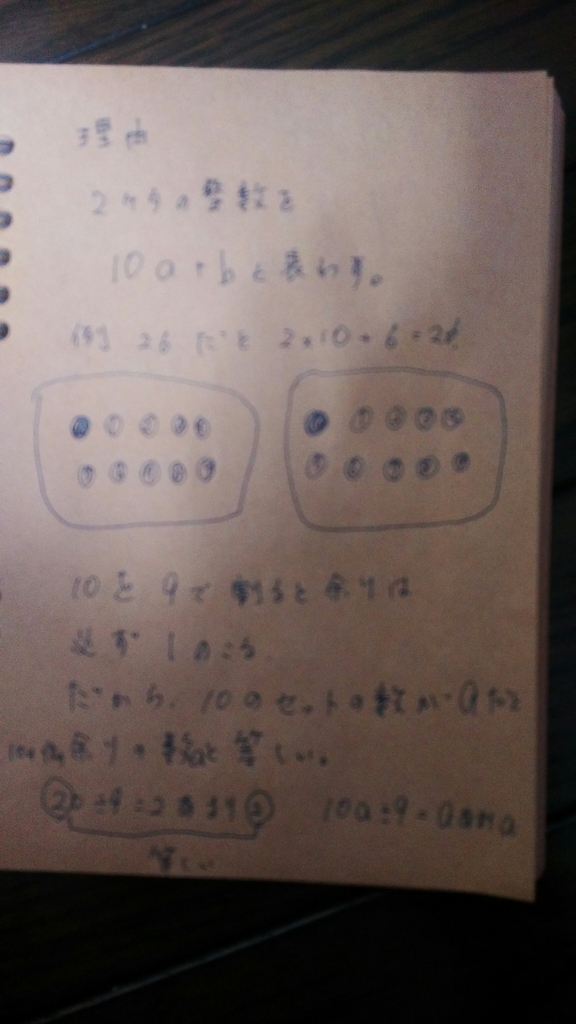
わたしにわかったことは、二桁の数を9で割ると、それぞれの位の数を足した数(をさらに9で割った数)があまりになること。
26だったら、9で割ったあまりは8になる。
62だったら、9で割ったあまりは、8になる。
それは、10を9で割ると、あまりは、必ず1になるから。
10の2倍、つまり20を割れば、あまりは2になる。
10の3倍、30を割れば、あまりは3になる。
10のセット数の数が、9で割ったときのあまりの数になる。
だから、そのあまりの数と、一の位の数を足すと、全体のあまりになる。
89だったら、9で割ると、8+9=17になる。それをさらに割ると、あまりは8になる。
89÷9=9あまり8だから、やっぱり成り立つ。
98÷9=9あまり8。

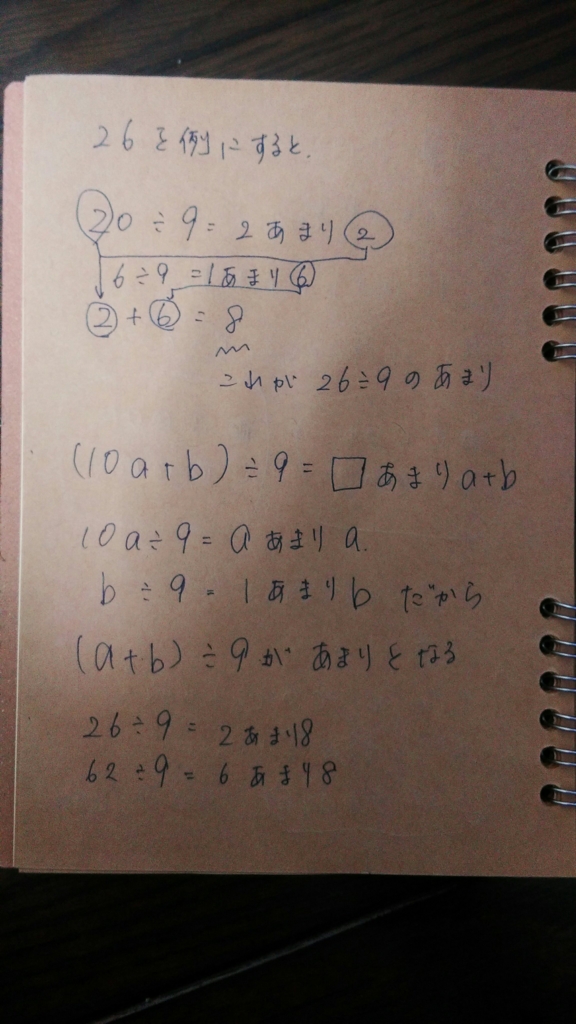
広告

100a+10b+c
=9(11a+b)+(a+b+c)
となりますので。3桁でも成立しますよ。
見てわかる通り、どんな桁数でも成立します。